Faserbeugung ist ein Verfahren zur Untersuchung molekularer Strukturen durch die Analyse von Beugungsbildern. Diese Bilder entstehen bei Durchstrahlung der Probe. Dazu werden meist Röntgenstrahlen, Elektronen oder Neutronen benutzt,[1] Die Besonderheit der Faserbeugung besteht darin, dass sich das Streubild nicht ändert, wenn die Probe um eine bestimmte Achse (die Faserachse) rotiert wird. Solche uniaxiale Symmetrie ist typisch für Filamente oder Fasern aus biologischen oder synthetischen Makromolekülen (Polymeren, Kunststoffen). Für die Kristallographie stellt Fasersymmetrie eine Erschwernis bei der Bestimmung der Kristallstruktur dar. Gegenüber dem Beugungsdiagramm des Einkristalls sind die Reflexe im Faserdiagramm verschmiert und können einander überlagern. Die Materialwissenschaft betrachtet Fasersymmetrie als Vereinfachung, denn nahezu die komplette zugängliche Strukturinformation ist in einem einzigen zweidimensionalen (2D) Beugungsbild enthalten. So ein Bild wird auf fotografischem Film oder einem 2D Detektor (wie bei einer Digitalkamera) belichtet. 2 anstatt 3 Koordinatenachsen reichen zur Beschreibung von Faserbeugung aus.
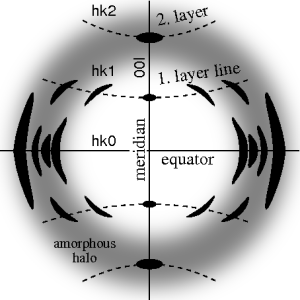
Das ideale Faserstreubild zeigt 4-Quadrantensymmetrie. In einem solchen Bild heißt die Richtung der Faserachse Meridian, die Richtung senkrecht hierzu ist der Äquator. Herrscht Fasersymmetrie, dann zeigen sich im 2D-Bild viel mehr Reflexe (beleuchtete "Punkte") gleichzeitig als im Beugungsbild des Einkristalls. Diese Reflexe erscheinen offensichtlich auf Linien (Schichtlinien) angeordnet, die ungefähr parallel zum Äquator verlaufen. So wird im Faserbeugungsbild das Schichtlinienkonzept der Kristallographie augenfällig. Die Biegung der Schichtlinien ergibt sich bei Verwendung eines ebenen Films oder Detektors; das Beugungsbild muss entzerrt werden, um gerade Schichtlinien zu erhalten. Reflexe werden identifiziert durch Laue-Indizes hkl (sie entsprechen den Millerschen Indizes, sind jedoch nicht teilerfremd). Dies sind 3 Ziffern. Reflexe auf der i-ten Schichtlinie haben l=i, wenn die Faserachse der kristallographischen c-Achse entspricht. Reflexe auf dem Meridian sind 00l-Reflexe. Künstliche Faserbeugungsbilder werden auch in der Kristallographie erzeugt (Drehkristallmethode). Dabei wird ein Einkristall im Röntgenstrahl um eine Achse rotiert.
Reale Faserstreubilder erhält man im Experiment. Sie zeigen nur Spiegelsymmetrie, weil die Faserachse nicht perfekt senkrecht zum einfallenden Strahl orientiert ist. Die entsprechende geometrische Verzerrung ist ausführlich von Michael Polanyi im Kaiser-Wilhelm-Institut für Faserstoffchemie unter dem Leiter Reginald Oliver Herzog studiert worden. Zur Beschreibung der Geometrie hat er das elegante Konzept der Polanyi-Kugel (ursprünglich: „Lagenkugel“) eingeführt. Später haben Rosalind Franklin und Raymond Gosling auf der Basis eigener geometrischer Überlegungen eine Näherungsformel zur Bestimmung des Faserkippwinkels β angegeben. Im ersten Analyseschritt wird das Faserstreubild entzerrt und auf die repräsentative Faserebene abgebildet. Diese ist die Ebene, welche die Zylinderachse des reziproken Raums enthält. In der Kristallographie wird zunächst eine Näherung der Abbildung in den reziproken Raum berechnet, die iterativ verfeinert wird. Das oft als Fraser-Korrektur bezeichnete digitale Verfahren startet mit der Franklin-Approximation. Es eliminiert die Verkippung, entzerrt das Bild und korrigiert die Streuintensität. Die korrekte Formel für die Bestimmung von β wurde von Norbert Stribeck angegeben.
- ↑ Mohamed Saad: Low resolution structure and packing investigations of collagen crystalline domains in tendon using Synchrotron Radiation X-rays, Structure factors determination, evaluation of Isomorphous Replacement methods and other modeling. PhD Thesis, Université Joseph Fourier Grenoble I, Oktober 1994, doi:10.13140/2.1.4776.7844 (google.com).
